µArt.cz

Pokud s mikrokontroléry neřešíte jenom blikání s LED, ale občas zabrousíte i do zpracování signálů, pravděpodobně jste již někdy v minulosti řešili výpočty trigonometrických funkcí.

V tomto článku popíšu základní princip algoritmu CORDIC pro iterativní výpočet funkcí sin a cos a také předvedu jednoduchou implementaci v jazyce C, vhodnou např. do mikrokontrolérů.

Co je to CORDIC?

Zkratka CORDIC znamená COordinate ROtation DIgital Computer a jedná se o výpočetní algoritmus především k výpočtu trigonometrických funkcí. Výpočet probíhá iterativně, to znamená v postupných krocích, a s předem známou přesností.

Algoritmus je relativně jednoduchý, ale velmi univerzální. Dá se upravit na výpočet hyperbolických funkcí, logaritmických funkcí, výpočet úhlu v komplexních číslech a pod. Celý výpočet navíc využívá jednoduchých operací (sčítání, odčítání, bitový posun), takže se hodí i pro hardwarovou implementaci. Toho využívají kalkulačky i zákaznické obvody, které mají omezené hardwarové prostředky (počet hradel je velmi malý, CORDIC nepotřebuje ani násobičku).

My si ukážeme implementaci CORDICu pro výpočet funkcí sin a cos.

Princip algoritmu

Samotný princip algoritmu není nijak složitý a k jeho vysvětlení nám postačí středoškolská matematika.

Základem CORDICu pro výpočet funkcí sinus a cosinus je jednotková kružnice. Libovolný bod na této kružnici můžeme vyjádřit v polárních i kartézských souřadnicích. V polárních nás bude zajímat úhel φ tohoto bodu a v kartézských zase hodnoty na osách X a Y. Sinus úhlu φ pak najdeme na ose Y a cosinus na ose X. Například bod s úhlem 90 stupňů, nebo také ^π/₂, leží přímo na ose Y a tedy hodnota sinus je rovna jedné, zatímco hodnota cosinus je rovna nule.

Algoritmus CORDIC v několika krocích rotuje bod na jednotkové kružnici o předem vypočítané úhly δ a jakmile je úhel φ ten, který hledáme, máme i hodnoty souřadnic x a y, které reprezentují cos a sin.

A teď, jak implementovat rotaci bodu pomocí sčítání a bitových posunů?

Představte si bod A vyjádřený v kartézských souřadnicích, to znamená A[x0, y0]. Takovýto bod lze vyjádřit i v polárních souřadnicích jako úhel od kladné horizontální osy a vzdálenost od počátku souřadnicového systému. Tuto situaci ilustruje obrázek níže, na kterém je bod A zanesen v obou systémech.

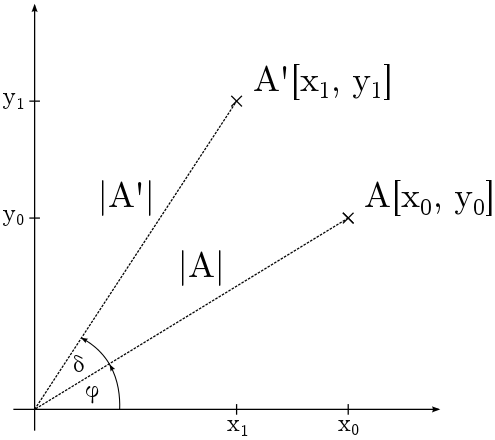
Pro převod z polárních na kartézské souřadnice platí:

\(
x_0 = |A| \cdot \cos(\varphi) \\
y_0 = |A| \cdot \sin(\varphi)
\)

Pokud budeme chtít bod A rotovat na pozici bodu A' tak, jak ukazuje obrázek, nejjednodušeji to provedeme v polárních souřadnicích. Vzdálenost |A| zůstává zachována, mění se pouze úhel:

\(
x_1 = |A| \cdot \cos(\varphi + \delta) \\
y_1 = |A| \cdot \sin(\varphi + \delta)
\)

Pojďme ještě dále a vyjádřeme si hodnoty funkcí sinus a cosinus pro sčítání úhlů. Vztahy sice vypadají na první pohled složitě, ale postupně se nám zjednodušší.

\(
\sin(\varphi + \delta) = \sin(\varphi) \cos(\delta) + \cos(\varphi) \sin(\delta) \\
\cos(\varphi + \delta) = \cos(\varphi) \cos(\delta) – \sin(\varphi) \sin(\delta)
\)

A teď se nelekněte, následuje trocha odvozování.

\(
x_1 = |A| \cdot \cos(\varphi + \delta) \\
x_1 = |A| \cdot [\sin(\varphi) \cos(\delta) + \cos(\varphi) \sin(\delta)] \\
x_1 = |A| \sin(\varphi) \cos(\delta) + |A| \cos(\varphi) \sin(\delta) \\
x_1 = x_0 \cos(\delta) – y_0 \sin(\delta)
\)

Pro y1 je postup podobný, takže jenom výsledek

\(
y_1 = y_0 \cos(\delta) + x_0 \sin(\delta)
\)

Jednoduše jsme roznásobili výraz a dosadili první vztah v tomto článku. Jak si můžete všimnout, výsledek neobsahuje ani vzdálenost |A|, ani původní úhel φ. Rotace bodu kolem počátku souřadnicového systému lze vyjádřit pouze pomocí původních kartézských souřadnic a hodnotou sinus a cosinus nového úhlu.

K čemu je nám to dobré? Už se k tomu dostáváme. Přepišme si předchozí odvozené vztahy do matic:

\(
\textbf{A}_1 = \textbf{R} \textbf{A}_0
\)

pro rotaci R pak platí (porovnejte s odvozenými vztahy výše)

\(
\textbf{R} = \left[\begin{matrix}
\cos(\delta) & -\sin(\delta) \\
\sin(\delta) & \cos(\delta)
\end{matrix}\right]
\)

Abych to dále nezdržoval a neodradil zbytečnou matematikou (zájemci si mohou celé odvození přečíst třeba na Wikipedii, článek o CORDIC), přeskočím až na to podstatné. Další trigonometrickou magií upravíme předchozí výrazy do následujícího tvaru:

\(
\textbf{R} = {1 \over \sqrt{1 + \tan(\delta)^2}} \begin{bmatrix} 1 & -\tan(\delta) \\ \tan(\delta) & 1 \end{bmatrix}
\)

Prostě mi věřte, že tomu tak je :) Nyní přichází to podstatné z CORDIC algoritmu: Jak celý výpočet ještě zjednodušit? To znamená, jak vypustit výpočet tangenty? Můžeme si předem vypočítat a do paměti uložit úhly a jejich odpovídající hodnoty tangens. Pak si vystačíme jenom s násobením těchto hodnot. Navíc, pokud si předem vypočítáme jen takové úhly δ, jejichž tangens nabývá hodnot záporných mocnin dvojky, vystačíme si jenom s bitovým posunem (tím jsme se zbavili i násobení a algoritmus tak bude ještě rychlejší a méně náročný na hardwarové zdroje).

Libovolný úhel δ, jehož hodnoty sinus a cosinus hledáme, lze postupně z těchto dovolených úhlů složit (δ = δ₁ + δ₂ + δ₃ + … + δ_n). Výpočet pak probíhá v iteracích a v řeči matematiky to můžeme zapsat jako:

\(
\left[\begin{matrix}
x_{i} \\ y_{i}
\end{matrix}\right] =
K_i \left[\begin{matrix} 1 & -\sigma_i 2^{-i} \\
\sigma 2^{-i} & 1
\end{matrix}\right]
\left[\begin{matrix} x_{i-1} \\ y_{i-1} \end{matrix}\right]
\)

kde i je i-tá iterace, σ nabývá pouze hodnot 1 nebo -1 a určuje, jestli se současná iterace bude od předchozího výsledku odečítat nebo přičítat a pro K_i platí

\(
K_i = {1 \over \sqrt{1 + 2^{-2i}}}
\)

Během výpočtu můžeme konstantu K ignorovat a vynásobit jí výsledek až na závěr. Navíc, K velmi rychle konverguje k hodnotě 0,60725293501, takže pro větší počty iterací můžeme v paměti uložit tuto jedinou hodnotu a tím zmenšíme nároky na pamět.

Úhly odpovídající záporným mocninám dvojky tangenty a konstantu K si předem vypočítáme pro potřebný počet kroků i a výsledky uložíme do paměti MCU. V jazyce C to může vypadat třeba takto:

/**
 * Úhly odpovídající atan(2.^-(i)) pro i < 10 
 */
static const double angles[] =  {
    0.78539816339745, 0.46364760900081,
    0.24497866312686, 0.12435499454676,
    0.06241880999596, 0.03123983343027,
    0.01562372862048, 0.00781234106010,
    0.00390623013197, 0.00195312251648
};

/**
 * Hodnoty K pro i < 10
 */
static const double K[] = {
    0.70710678118655, 0.63245553203368,
    0.61357199107790, 0.60883391251775,
    0.60764825625617, 0.60735177014130,
    0.60727764409353, 0.60725911229889,
    0.60725447933256, 0.60725332108988
};

A samotný výpočet v jazyce C může vypadat takto (kód jsem psal především aby byl čitelný, proto jsem nijak neoptimalizoval a použil jsem místy hodně neúsporný zápis):

#define MAX_I  (10)
#define K10    (0.60725332108988)

/*
 * Funkce vypočítá hodnoty sinus a cosinus úhlu
 * delta (v radiánech).
 *
 * Počet iterací je MAX_I,
 * úhel může ležet pouze v prvním a čtvrtém
 * kvadrantu, pro druhý a třetí je nutné
 * posunout úhel delta a poté změnit znaménko
 * výsledků.
 */
void cordic(double delta) {
    uint8_t i;
    uint8_t sigma = 1;
    double power_of_two = 1;

    /* Začneme s hodnotou sinus=0.0, cosinus=1.0 */
    double xi=1.0;
    double yi=0.0;

    for (i=0; i < MAX_I; i++) {
      /* Pokud je úhel záporný, budeme odčítat */
      if (delta < 0) {
        sigma = -1;
      /* jinak přičítat */
      } else {
        sigma = 1;
      }      

      /* Výpočet nových hodnot xi a yi */
      double factor = power_of_two * sigma;
      double tmp1 = xi - yi * factor;
      double tmp2 = yi + xi * factor;
      xi = tmp1;
      yi = tmp2;

      /* Zbývající úhel */
      delta = delta - sigma * angles[i];

      /* Záporná mocnina dvojky */
      power_of_two = power_of_two / 2;
    } /* end for */

    /* Na závěr vynásobíme konstantou K pro i=MAX_I=10 */
    yi = yi * K10;
    xi = xi * K10;

    /* Výsledek výpočtu je v proměnných xi a yi: */
    /*   sin(delta) = yi */
    /*   cos(delta) = xi */
}

Pokud tento kód implementujete do libovolného AVR, bude algoritmus fungovat s relativně dobrou přesností. Větší přesnost docílíte větším počtem iterací, čemuž ale odpovídá i delší výpočetní čas. Od určitého počtu iterací se už přesnost zvětšovat nebude, jelikož narazíte na maximální přesnost datového typu double.

Další problém takto napsaného algoritmu je použití datových typů double. Tento typ je číslo s plovoucí desetinou tečkou a práce s ním je pro malý 8bitový MCU velmi výpočetně náročná. Vhodnější se zde jeví použití pevné desetinné tečky, pro kterou má rodina AVR několik instrukcí a násobení dvou desetinných čísel s pevnou tečkou je tedy otázka jedné instrukce (viz application note AVR201: Using the AVR Hardware Multiplier; o tomto se moc nemluví, rád bych časem napsal článek s příklady).

Dále je algoritmus funkční pouze pro úhly z prvního a čtvrtého kvadrantu. Pro úhly z druhého a čtvrtého je nutné vstupní úhel delta posunout do vhodného kvadrantu a výsledku pak obrátit znaménko.

Závěr

Na závěr pár relevantních odkazů k tomuto tématu:

• Seriál Fixed point arithmetic na root.cz
• AVR200: Multiply and Divide Routines
• AVR201: Using the AVR Hardware Multiplier
• Sekce CORDIC z knihy Digital Circuits na wikibooks.org

Poznámka pro ty, kterým se nechce znovu vymýšlet kolo: Standardní knihovna math.h pro AVR rodinu již obsahuje funkce pro většinu používaných matematických funkcí, včetně několika užitečných konstant.

Poznámka pro ty, kterým se chce znovu vymýšlet kolo: Co si třeba napsat CORDIC pro logaritmus? Nebo si výše popsaný algoritmus přepsat do assembleru?