Metoda smyčkových proudů II.

V minulém příspěvku jsme si popsali co to je MSP, jak a na co se dá použít a také jsme si vyřešili jednoduchý příklad s jedním zdrojem napětí. Jak se ukázalo, téma je to velmi žádané a spousta studentů si s ním neví rady. Rozhodl jsem se proto napsat pokračování, ve kterém si vyřešíme můstkové zapojení pomocí MSP. Pojďme na to!

Můstkové zapojení

Nejdříve si stručně řekněme jak takové můstkové zapojení vypadá a k čemu je dobré. Na obrázku níže je vidět můstek složený z 5 rezistorů a jednoho zdroje napětí (pro jednoduchost budeme uvažovat pouze rezistivní zátěž a stejnosměrný proud).

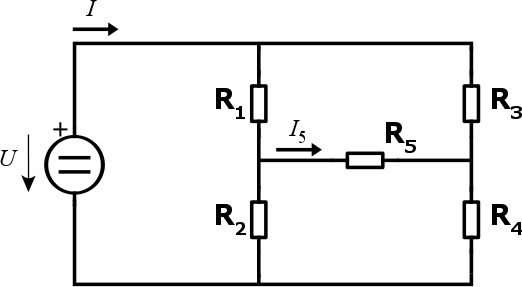
Tato zapojení se často používají pro nejrůznější měření (například měření kmitočtu pomocí Wienova můstku, měření odporů  Wheatstoneovým můstkem nebo Thomsonovým můstkem, měření kapacit Scheringovým můstkem a mnoho dalších) nebo jako usměrňovače  (pokud jste si někdy konstruovali stabilizovaný zdroj, pak jste nejspíše k usměrnění střídavého napětí použili diodový můstek, také známý jako Graetzův).

Jestli studujete nebo chcete studovat elektrotechniku, jistě se s můstky setkáte a budete je používat. Ještě teď si pamatuji, jak jsem se dlouho do noci učil nejrůznější můstková zapojení na zkoušku z měření :)

Volba smyček

Teď již víme jak můstkové zapojení vypadá, pojďme vyřešit následující problém:

Chceme spočítat proud I₅ a úbytek napětí U₅ na rezistoru R₅.

Prvním krokem, který je při MSP vždy nejdůležitější, je volba nezávislých smyček. Při pohledu na zapojení vidíme, že obsahuje 3 nezávislé smyčky. Dokonce si můžeme vybrat, protože jsou zde možné 2 způsoby. Jedním z nich je:

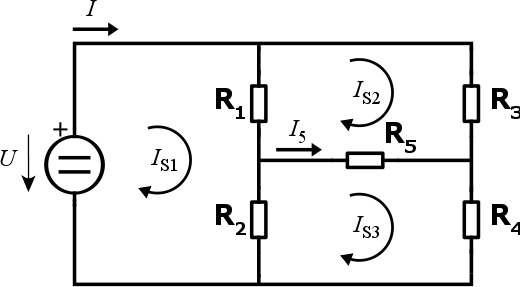
Všimněte si, že jsme všem smyčkám přiřadili stejnou orientaci. To sice není nutné, ale jak jsme si v minulém díle řekli, ulehčí nám to práci se znaménky a výrazně sníží riziko chyby.

Teď si na papír napište všechny tři rovnice, které odpovídají jednotlivým smyčkám. Jakmile je budete mít, podívejte se na moje a zkontrolujte výsledek:

Smyčka I_S1:

\(
\begin{array}{l}
– U + R_1 (I_{S1} – I_{S2}) + R_2 ( I_{S1} – I_{S3} ) = 0 \\
R_1 I_{S1} – R_1 I_{S2} + R_2 I_{S1} – R_2 I_{S3} = U_0 \\
I_{S1} (R_1 + R_2) + I_{S2} (-R_1) + I_{S3} (-R_3) = U_0 \\
\end{array}
\)

Smyčka I_S2 (jak upravit tvar rovnice do vhodného tvaru jsme si ukázali u předchozí smyčky, proto teď už jen výsledek):

\(
\begin{array}{l}
I_{S1} (-R_1) + I_{S2} (R_1 + R_3 + R_5) + I_{S3} (-R_5) = 0
\end{array}
\)

Smyčka I_S3:

\(
\begin{array}{l}
I_{S1} (-R_2) + I_{S2} (- R_5) + I_{S3} (R_2 + R_5 + R_4) = 0
\end{array}
\)

A hotovo. Nejtěžší část máme za sebou, teď už jenom výpočet. K tomu doporučuji použít Cramerovo pravidlo, které pracuje s maticemi. Ty budou v našem případě vypadat následovně:

\(
\left[\begin{matrix}
R_1 + R_2 & -R_1 & -R_2 \\
-R_1 & R_1+R_3+R_5 & -R_5 \\
-R_2 & -R_5 & R_2+R_5+R_4 \\
\end{matrix}\right] \cdot
\left[\begin{matrix}
I_{S1} \\
I_{S2} \\
I_{S3} \\
\end{matrix}\right] =
\left[\begin{matrix}
U_0 \\
0 \\
0 \\
\end{matrix}\right]
\)

Pokud se pozorně podíváte na všechny tři matice, zjistíte, že se jedná o obyčejný Ohmův zákon R · I = U. Cramerovo pravidlo používá k výpočtu determinanty matic. Jednotlivé determinanty se dají spočítat následovně:

\(
\det_1 = \left[\begin{matrix}
U_0 & -R_1 & -R_2 \\
0 & R_1+R_3+R_5 & -R_5 \\
0 & -R_5 & R_2+R_5+R_4 \\
\end{matrix}\right] \\
\det_2 = \left[\begin{matrix}
R_1 + R_2 & U_0 & -R_2 \\
-R_1 & 0 & -R_5 \\
-R_2 & 0 & R_2+R_5+R_4 \\
\end{matrix}\right] \\
\det_3 = \left[\begin{matrix}
R_1 + R_2 & -R_1 & U_0 \\
-R_1 & R_1+R_3+R_5 & 0 \\
-R_2 & -R_5 & 0 \\
\end{matrix}\right]
\)

Všimněte si, že u každého determinantu nahradíme itý sloupec za napěťovou matici U. Výpočet jednotlivých smyček je teď otázkou výpočtu determinantů a jejich podílu:

\(
I_{S1} = \frac{\det_1}{\det}
\)
\(
I_{S2} = \frac{\det_2}{\det}
\)
\(
I_{S3} = \frac{\det_3}{\det}
\)

Výsledek

Ze zadání nás zajímá pouze proud a napětí na rezistoru R₅. Jelikož jsme neměli zadané žádné konkrétní hodnoty rezistorů ani napětí zdroje, spokojíme se pouze s konstatováním, že:

\(
I_5 = I_{S3} – I_{S2} = \frac{\det_3}{\det} – \frac{\det_2}{\det}
\)

A tím máme hotovo!

Jiný způsob řešení

Na začátku jsme si řekli, že obvod má dva způsoby, jakým můžeme zvolit nezávislé smyčky. Ukažme si jej:

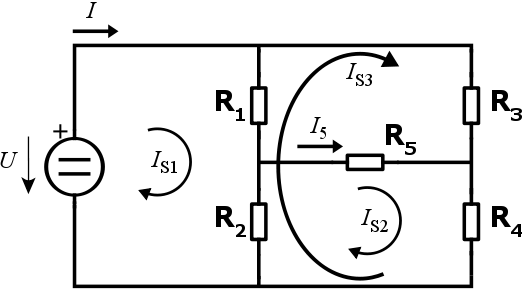
I toto je možné a pro náš příklad i výhodnější. Pokud se pozorně podíváte na smyčky, zjistíte, že pro výpočet proudu I₅ nám stačí spočítat jednu smyčku a tím pádem nám odpadne výpočet dalšího determinantu. Pokud počítáte na kalkulačce, ušetří vám to mnoho práce:

\(
I_5 = I_{S2}= \frac{\det_2}{\det}
\)

Proto je vhodné při výběru smyček vždy uvažovat.

Závěr

V tomto článku jsme si vyřešili můstkové zapojení pomocí metody smyčkových proudů. Zároveň jsme si ukázali Cramerovo pravidlo, kterým můžeme jednoduše spočítat proudy smyček. Také jsme si ukázali, že jeden obvod nemusí mít vždy jen jedno řešení a že je vhodné při výběru smyček přemýšlet a ulehčit si později práci.

V našem povídání o MSP jsme zatím úplně vynechali obvody s více zdroji (sice je to principiálně stejné, ale dělají se v tom chyby) a zdroji proudu (v takovém případě je totiž nutné proudové zdroje přepočítat na jejich ekvivalentní napěťové modely). O tom možná až příště.

Ještě chci upozornit, že nemám patent na rozum a nevylučuji, že jsem se nekde při výpočtu zmýlil. Budu proto rád, když na případně chyby upozorníte. Buď na webu qa.uart.cz formou otázky, nebo přímo na můj email slintak(at)uart(dot)cz.

Články v sérii

<< Metoda smyčkových proudůMetoda postupného zjednodušování >>