Metoda postupného zjednodušování

Před nějakou dobou jsem zde psal o metodě smyčkových proudů (a zde druhý díl), kde jsem ukázal jak lze metodu použít k analýze jednoduchého elektrického obvodu. Ti zkušenější z vás se možná podivovali, proč jsem na takový jednoduchý obvod (s jedním zdrojem napětí) zvolil právě MSP. Ano, máte pravdu, v případě obvodu s jedním zdrojem je výhodnější a rychlejší použít metodu postupného zjednodušování. Pojďme si ji tedy ukázat.

Jako příklad nám poslouží obvod, se kterým jsme již počítali MSP.

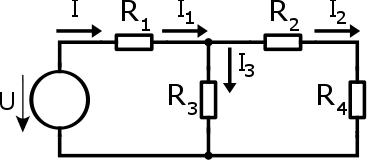
Tento obvod není zrovna typickým příkladem pro MSP, jelikož obsahuje pouze jeden zdroj napětí. Smyčkové proudy ukazují svou sílu až v obvodech, kde je zdrojů více, často také obsahují zdroje proudu a další chytáky. Metoda postupného zjednodušování je naopak založena na předpokladu, že lze v obvodu nalézt sériové a paralelní kombinace rezistorů. V zapojení výše je tento předpoklad splněn, a proto si na něm MPZ ukážeme.

Předpokládám, že čtenář je seznámen s pojmy sériové a paralelní zapojení rezistoru a umí je spočítat. V opačném případě odkážu na články sériové zapojení a paralelní zapojení na Wikipedii.

 Zadání

Zadání našeho příkladu je prosté:

Spočítejte proud a napětí na rezistoru R_4.

Jelikož je v zapojení pouze jeden zdroj napětí a sério-paralelní kombinace 4 rezistorů, zvolíme metodu postupného zjednodušování.

Řešení

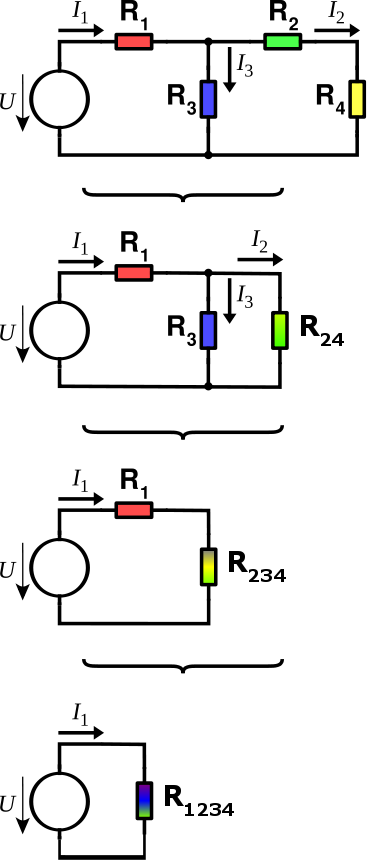
Nakreslete si obvod na papír a začněte v něm hledat sériové a paralelní kombinace rezistorů. Naším cílem je postupně obvod zjednodušit do takového tvaru, aby obsahoval jeden zdroj napětí a jeden rezistor.

Na první pohled vidíme, že rezistory R₂ a R₄ jsou zapojeny sériové. Vytvoříme z nich proto rezistor označený R₂₄, který bude mít následující hodnotu:

\(
R_{24} = R_2 + R_4
\)

Teď nám v obvodu vzniklo paralelní spojení rezistorů R₃ a R₂₄, které spočítáme:

\(
R_{234} = R_3 || R_{24} = \frac{R_3 \cdot R_{24}}{R_3 + R_{24}}
\)

Teď už nám zbývají dva sériově zapojené rezistory:

\(
R_{1234} = R_1 + R_234
\)

Výsledná hodnota rezistoru R₁₂₃₄ je tedy:

\(
R_{1234} = R_1 + \frac{R_3 \cdot (R_2 + R_4)}{R_3 + (R_2 + R_4)}
\)

Už máme skoro hotovo. Zbývá nám jenom spočítat úbytek napětí a proud rezistorem R₄ a máme splněno zadání. Označme si proto hledané veličiny jako U₄ a I₄.

Při pohledu na schéma je zřejmé, že proud I₄ je stejný jako I₂. Napětí U₄ můžeme spočítat například:

\(
U_4 = R_4 \cdot I_4 = R_4 \cdot I_2
\)

Chybí nám tedy proud I₂. Naštěstí jej můžeme jednoduše spočítat:

\(
I_2 = \frac{U_3}{R_{24}}
\)

Stále nám chybí U₃. To můžeme spočítat dvěma způsoby. Buď jako rozdíl napětí na zdroji a úbytku U₁ na rezistoru R₁, nebo jako napětí na děliči tvořeném rezistory R₁ a R₂₃₄. Ukážeme si obě možnosti:

\(
U_3 = U – U_1 = U – R_1 \cdot I_1 = U – R_1 \cdot \frac{U}{R_{1234}} \\
U_3 = U \cdot \frac{R_1}{R_1 + R_{234}}
\)

A to je vše. Úspěšně jsme obvod zjednodušili a spočítali všechny neznámé. Pro jistotu zde ještě jednou napíšu postup jak spočítat proud a napětí na R₄. Takže:

Nejdříve spočítat napětí U₃ jako napětí na děliči. Odtud spočítáme proud I₂, což je také hledaný proud I₄. A nakonec napětí U₄.

Pokud si nevšimnete, že napětí U₃ se dá spočítat pomocí děliče, pak je postup následovný:

Spočítat celkový proud obvodem I₁. Odtud úbytek napětí na R₁. Napětí U₃ je rozdílem U a U₁. Odtud spočítáme proud I₂, což je také hledaný proud I₄. A nakonec napětí U₄.

A tím máme konečně hotovo.

Výsledek

Ještě uvedu konečný výsledek:

\(
I_4 = I_2 = \frac{U_3}{R_{24}} = \frac{U \frac{R_{234}}{R_1 + R_{234}}}{R_{24}} \\
U_4 = R_4 \cdot I_2
\)

Závěr

Výše popsaná metoda se hodí všude tam, kde můžeme najít sériové a paralelní kombinace rezistorů a ty postupně zjednodušit na rezistor jediný. Všimněte si, že jsme si při práci vystačili se sčítáním, násobením a dělením. Oproti smyčkovým proudům, kde musíme řešit několik rovnic o několika neznámých je tato metoda výrazně jednodušší.

Pokud máte na výběr, je vhodné se před samotnou analýzou obvodu zamyslet a zvolit tu nejjednodušší cestu, která se nabízí.

Články v sérii

<< Metoda smyčkových proudů II.