µArt.cz

Metoda smyčkových proudů, často také zkracována na MSP, využívá II. Kirchhoffův zákon a používá se tehdy, pokud potřebujeme zjistit všechny neznámé (úbytky napětí a proudy na jednotlivých prvcích) v obvodu.
Metodu lze využít jak v stejnosměrných, tak ve střídavých obvodech. V druhém případě je však postup výpočtu obtížnější kvůli výskytu komplexních čísel. Pro jednoduchost se budeme zabývat pouze stejnosměrnými obvody.

II. Kirchhoffův zákon

Nejprve si připomeneme druhý Kirchhoffův, který nám říká:

Součet úbytků napětí v uzavřené smyčce je roven nule.

To znamená, že v uzavřeném obvodu se nemůže napětí nikde ztratit, na všech prvcích obvodu dohromady tedy naměříme stejné napětí, jaké nám dává zdroj (případně zdroje). Ukažme si to na jednoduchém příkladu:

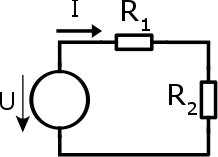
V tomto jednoduchém obvodě je jeden ideální zdroj napětí U a dva, do série zapojené rezistory R1 a R2. Obvodem teče proud I, úbytky napětí na rezistorech označme U1 a U2.

V obvodu je jediná uzavřená smyčka, ve které je podle II. KZ součet napětí roven nule. Pojďme si napsat rovnici, která nám toto tvrzení dokáže:

\(
\begin{array}{l}
U – U_1 – U_2 = 0 \\
U – I \cdot R_1 – I \cdot R_2 = 0 \\
U – I \cdot ( R_1 + R_2 ) = 0
\end{array}
\)

Co jsme to udělali? Nejprve jsme vytvořili rovnici podle smyčky v obvodu. Od zdroje napětí U jsme postupně odečetli všechny spotřebiče, tedy R1 a R2. Následně jsme za tyto úbytky napětí dosadili (podle Ohmova zákona) součin proudu obvodem a rezistivity jednotlivých rezistorů. Nakonec jsme v druhé rovnici vytkli proud I a získali jsme poslední, třetí rovnici.

Jednoduchý příklad MSP

Teď již víme co to je II. KZ a jak se vytvoří rovnice uzavřené smyčky v obvodu. V praxi se často setkáváme se složitějšími obvody, ve který je více uzavřených smyček (mnohdy jsou na sobě smyčky závislé, viz dále). Pokud bychom všechny tyto smyčky vyjádřili tak jak jsme to udělali výše, získáme soustavu několika rovnic o více neznámých, které lze jednoduše řešit.

V předchozím odstavci jsme si vysvětlili jak funguje MSP. Pojďme si nově nabyté znalosti ukázat na příkladu, ve kterém lze nalézt dvě nezávislé smyčky (poznámka o nezávislosti smyček je velmi důležitá a bude vysvětlena níže).

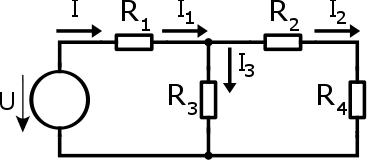
Tento jednoduchý obvod obsahuje jeden ideální zdroj napětí U a čtyři rezistory zapojené v sériově-paralelní kombinaci. Do obvodu jsme si zároveň vyznačili všechny proudy, které se v obvodu nacházejí. Právě jejich velikost se budeme snažit zjistit.

Nalezení nezávislých smyček

První krok při řešení obvodu pomocí MSP je označit si nezávislé smyčky, které si v našem příkladě označíme S1 a S2 a šipkou zvolíme jejich orientaci (orientaci proudových smyček lze zvolit libovolně, během dalších kroků je ale nutné si hlídat znaménka).

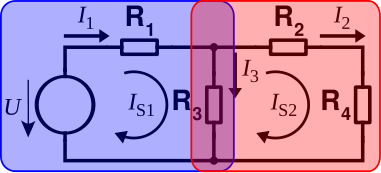
Vyjádření rovnic všech smyček

Teď máme vše potřebné, abychom pro tyto proudové smyčky vytvořili rovnice. Postup je stejný jako jsme si ukázali u II. KZ — zapíšeme si všechny prvky, které se v dané smyčce nalézají. Pokud má úbytek napětí na prvku stejnou orientaci jako smyčka, přidáme jej do obvodu s kladným znaménkem, v opačném případě se záporným.

První smyčka S1

První proudová smyčka, označená jako S1, teče přes tři prvky — jeden zdroj a dva spotřebiče. Podle již zmíněného pravidla tyto prvky zapíšeme do rovnice, která je rovna nule a postupně ji budeme vyjadřovat a upravovat:

\(
\begin{array}{l}
– U + U_1 + U_3 = 0 \\
– U + R_1 I_{S1} + R_3 ( I_{S1} – I_{S2} ) = 0 \\
– U + R_1 I_{S1} + R_3 I_{S1} – R_3 I_{S2} = 0 \\
– U + ( R_1 + R_3 ) I_{S1} – R_3 I_{S2} = 0 \\
( R_1 + R_3 ) I_{S1} – R_3 I_{S2} = U
\end{array}
\)

Druhá smyčka S2

Zde je postup stejný jako u první smyčky, pouze s tím rozdílem, že máme tři spotřebiče a žádný zdroj:

\(
\begin{array}{l}
R_3 ( I_{S2} – I_{S1} ) + R_2 I_{S2} + R_4 I_{S2} = 0 \\
R_3 I_{S2} – R_3 I_{S1} ) + R_2 I_{S2} + R_4 I_{S2} = 0 \\
– R_3 I_{S1} + ( R_2 + R_3 + R_4 ) I_{S2} = 0
\end{array}
\)

Tímto jsme si zapsali rovnice obou proudových smyček a zároveň jsme je upravili, aby se nám později jednoduše počítalo. Na levé straně jsme nechali součiny proudů a rezistivit, na pravou stranu jsme převedli napěťové zdroje. Obě rovnice si pro přehlednost zapišme pod sebe:

\(
\begin{array}{l}
( R_1 + R_3 ) I_{S1} – R_3 I_{S2} = U \\
– R_3 I_{S1} + ( R_2 + R_3 + R_4 ) I_{S2} = 0
\end{array}
\)

Máme dvě rovnice o dvou neznámých (hledáme velikost proudových smyček S1 a S2, velikost zdroje a rezistorů považujme za známé), které můžeme jednoduše vypočítat.

Pokud bychom měli složitější příklad, ve kterém se objeví více smyček, budeme mít i více rovnic a tím pádem i více neznámých. V takovém případě je vhodné vzniklou soustavu přepsat jako matici a řešit například pomocí Cramerova pravidla.

Nezávislé a závislé smyčky

Pokud jste si pozorně přečetli předchozí odstavce, jistě jste si všimli, že jsme použili výraz nezávislé smyčky.

Aby byla výsledná soustava rovnic, které podle smyček vytvoříme řešitelná, musíme zvolit smyčky, které na sobě nejsou závislé, tedy jejich velikost se nijak neovlivňuje. Pokud bychom zvolili špatně a velikosti zvolených smyček by na sobě závisely, výsledná soustava rovnic by nešla vyřešit.

V obvodu, na kterém jsme si podrobně ukázali postup MSP lze nalézt celkem tři smyčky, ale pouze dvě jsou nezávislé. Pojďme si ukázat nevhodně zvolené smyčky:

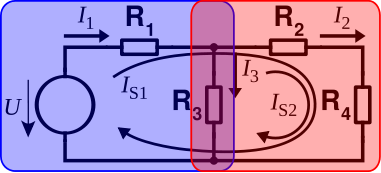
Pokud si zkusíte tento příklad vypočítat, zjistíte, že takto zvolené smyčky jsou závislé a vzniklá soustava rovnic nemá řešení.

Poznámky k MSP

Ačkoliv je jedno, jakou orientaci smyček zvolíme, je vhodné si stanovit pravidlo a toho se při řešení příkladu držet. Je vhodné si například volit orientaci vždy po směru hodinových ručiček, vyhnete se tím zbytečným chybám při zápisu znamének.

Také je vhodné volit nezávislé smyčky podle ok obvodu. V našem příkladě, který jsme výše řešili jsme zvolili obě proudové smyčky shodně s oběma oky, které se v obvodu nacházejí.

Dále je nutné si uvědomit, že tato metoda se dá použít pouze, pokud jsou v obvodu napěťové zdroje. Pokud se v obvodu nacházejí i proudové zdroje, je nutné je nejdříve přepočítat na jejich ekvivalentní napěťový zdroj.

Závěr

Metoda smyčkových proudů je vhodná pro jednoduché obvody, které chceme řešit ručně. U složitějších obvodů může být počet možných smyček a počet výsledných rovnic velký a tím pádem obtížně řešitelný. Také je nutné zdůraznit, že MSP se hodí pro lineární obvody (rezistory, transformátory, apod.), ale je naprosto nevhodná pro obvody s polovodičovými prvky, nebo integrovanými obvody.

Na závěr uveďme, že tato metoda je vhodná i pro střídavé obvody, pouze s tím rozdílem, že výsledné rovnice obsahují komplexní čísla. Jejich výpočet je tedy složitější, ale v principu stejný.

Články v sérii

Metoda smyčkových proudů II. >>